Significant Digits and Measurement
Question: What digits are significant when recording a measurement?
When scientists use an instrument, such as a ruler or graduated cylinder, the scientist can only measure as accurately as the instrument will allow. There is a proper way to record valid measurements from any instrument which includes numbers that are considered significant.
Part A - Econo Ruler
The ruler shown does not have very specific markings on it. As such, those students reading the ruler wrote different values for their measurement of a tile.
Sally: 3 cm
James 2.5 cm
Tony: 3.5 cm
Maria: 2 cm
Damien: 2.8 cm
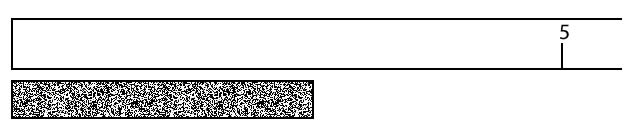
1. What distance can you be CERTAIN of for the length of the tile?
I can be certain that the length is between _____ and _____
2. What technique could students have used to determine an estimation for how long the tile was?
3. Which measurement do you agree with?
Part B - Basic Ruler
The students were able to find a better ruler, as shown below. Their measurements were recorded again.
Sally: 2.4 cm
James 2.75 cm
Tony: 2 cm
Maria: 2.3 cm
Damien: 2.4 cm
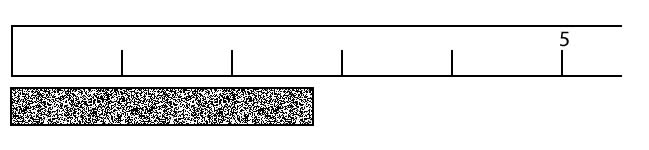
4. What distances can you be CERTAIN of on this ruler?
5. Were the students able to agree on a single value (1, 2, 3..) for any digit. If yes, what did they all agree on?
6. What feature of the Basic Ruler made it possible for the students to agree on a value?
7. There will always be uncertainty in any measurement. This causes variation in measurements even if people are using the same instrument. Compare the variation in the measurements made by the students. Which ruler resulted in greater variation and explain why this would be the case.
Part C - Best Ruler
Sally: 2.72 cm
James 2.75 cm
Tony: 2.73 cm
Maria: 2.7 cm
Damien: 2.752 cm

8. After the students obtained an even better ruler, were they able to agree on a single value for any of the digits in their measurements? What value(s) did they agree on?
9. What feature of this ruler made it possible for the students to agree on this value?
Further Analysis
When using measuring instruments, variation is expected. Everyone will estimate differently between marks on the instrument. However, digits that are CERTAIN (based on the marks on the instrument) should not vary from person to person.
10. What values are CERTAIN on the Best Ruler?
What numbers varied or were UNCERTAIN?
Part D - Valid Measurements
The measurements shown on the three rulers are compiled below. The measurements that follow the rules agreed upon by science are in the "valid" column. Those that do not follow the rules are in the "invalid" column.
Valid: 2 cm, 3, cm
Invalid: 2.5, 3.5, 3.8

Valid: 2.5 cm, 2.3 cm, 2.4 cm
Invalid: 2.75, 2

Valid: 2.72 cm, 2.73 cm, 2.75 cm
Invalid: 2.7, 2.752

11. For each valid measurement, draw a square around the CERTAIN digits (if any) and circle the digits that were estimated (if any).
12. Based on the examples in Part D, circle the phrase that best completes the sentence?
a) In a valid measurement, you record [ zero | one | two ] estimated digit(s).
b) In a valid measurement, the estimated digit is he [ first | second to last | last ] digit in the measurement.
c) In a valid measurement, the estimated digit depends on the [ number of marks on the ruler | the length of the ruler ].
d) The most precise instrument was [ Econo | Basic | Best ] ruler.
e) An advertisement for a digital scale claims that it measures to the nearest 10th of a kilogram. The scale would have which reading [ 50 kg | 50.2 kg | 50.21 kg ]
13. Explain why Tony's measurement of 2 on the Basic Ruler would be considered invalid.
14. James made a measurement on the Basic Ruler of 2.75 and it was considered invalid. Why was the same measurement on Best Ruler considered valid?
15. A student used on of the three rulers to measure the length of a caterpillar. The student recorded the length as 4.0 cm. Which ruler was the student using (assuming this is a valid measurement)?
16. Paula was catching up when she recorded the tile as measuring 2.69 cm using the Best Ruler. Her classmates thought this was wrong because her second digit was not "2". However, Paula's measurement is perfectly valid. Does valid mean that the number is accurate? Propose a definition of what a VALID number is.
Part E: Significant Digits
When a measurement is recorded properly, all of the digits that are read directly (CERTAIN) and one estimated (UNCERTAIN) digit are called significant digits. The number of allowable significant digits is determined by the marks of the instrument. Sometimes a "0" is the estimated digit and must be recorded.
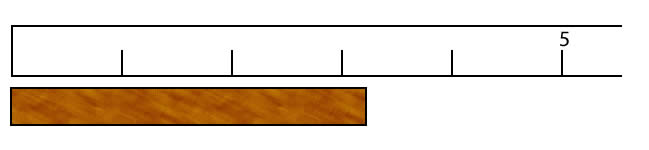
17. Record the length of the object to the proper number of significant digits for each ruler below.

Other Resources on Measuring
Measure a Bean - basic lab on measurements and collecting data
Tools and Measurements - how to use various tools in the lab, such as a graduated cylinder, ruler, and beaker
Using a Micropipette - activity explores how to use a micropipette to measure small volumes
Equipment Station Lab - a station lab activity where students move through stations and perform tasks with scientific equipment

