The Decay Curve of Twizzlers

Objectives: The learner will:

1. Identify an exponential decay curve
2. Given data, generate a graph showing exponential decay

Introduction

Radioactive isotopes all decay at a constant rate. While some can decay rapidly, others may decay over thousands of years. We measure the rate of decause using a unit called the half-life. The half-life of an isotope is the time it takes for one half of the substance to decay. For example...

Hydrogen-3 has a half-life of 12.3 years
Carbon-14 has a half-life of 5,730 years
Polonion-210 has a half-life of 140 days
Radon-222 has a half-life of 3.82 days

When we talk about decay, it does not mean that the isotope disappears, it actually changes into a new substance. A radioactive isotope continues to decause until it reaches a stable isotope, a process that is called a decay series. The stable, or most common form of carbon is Carbon-12. The number "12" refers to its atomic mass, its atomic number is 6, which means that the stable version has 6 protons and 6 neutrons, and an atomic mass of 12.

What does this have to do with carbon dating? Carbon dating uses the relative amounts of carbon 12 and carbon 14 to determine the age of a rock. Since it takes almost 6000 years for Carbon 14 to become Nitrogen-14, we can use the amount still within the rock to give us an idea of how old the rock is.

Key Points:

• All living things contain carbon.
• Isotopes are variations of an element; the number of protons in each isotope is the same, but the number of neutrons differs.
• Carbon has three natural isotopes: carbon-12, carbon-13, and carbon-14.
• Carbon-14 is a rare version of carbon with eight neutrons. It is radioactive and decays over time.
• When carbon-14 decays, a neutron turns into a proton and it loses an electron to become nitrogen-14.
• The length of time it will take for half the amount of carbon-14 to decay is known as its half-life.
• Carbon dating measures the ratio of carbon-14 to carbon-12 and uses the known half-life of carbon-14 to estimate the age of organic material

The Simulation: In this activity, you will simulate the radioactive decay of an isotope using Twizzlers and graph your results.

Procedure:

1. Assume that the half-life of a Twizzler is 30 seconds. This means that once you begin the lab, half of the Twizzler must decay every 30 seconds.
2. Using a ruler, measure the length of your Twizzler, this represents the length of time at 0 seconds (the beginning of the lab). Mark this on the graph.
3. Watch the clock or stopwatch, during the next 30 seconds, you must eat exactly half of your Twizzler, measure carefully with the ruler where half the twizzler lies. If you don't want to eat the twizzler, you can use scissors to cut it in half. Mark the length of the Twizzler now on the graph at the 30 second mark.
4. Repeate every 30 seconds, by halving your Twizzler. Stop when you get to 210 seconds.
5. Draw a smooth curve that connects your points on the graph.

Analysis

1. At this rate, will the twizzler ever disappear? Explain your answer.

 

2. If you had a giant, 1000 cm Twizzler, how much of it would remain after:

a) One half-life ____________________
b) Two half-lifes ___________________
c) Three half-lifes ___________________
d) Four half-lifes ___________________
e) Five half-lifes ___________________
f) Six half-lifes ___________________

3. Iodine-131 has a half life of about 8 days. If you had 60 grams of I-131, how much would remain after 24 days? Show your work.

 

4. Examine this graph showing the population growth of rabbits. Compare the shape of the graph to the graph you made on twizzlers. How are they similar and how are they different?

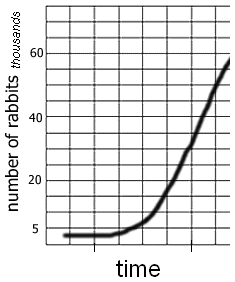
6. Both the Twizzler graph and the Rabbit Graph show a type of exponential growth or decay. In your own words, explain what "exponential" means.