Data Collection is Fun(gi)

Forms of fungi can be seen almost everywhere, and you may pass varieties of fungi on trees, logs, in your yard and not even take a moment to look at them. Some fungi are very tiny, even microscopic, others can be gigantic and even extend over large areas.

The fruiting bodies of fungi are formed when the fungi reproduces and are specific to each type of fungi, each can have differences in shape, color, width and height. Biologists who study fungi learn to identify a mushroom by the shape of its top, its coloration and other features that are unique to its species.

The following data was gathered by a field biologist who was searching for fungi specimens in a field. Your job is to design a table, chart or graph that will organize the data the biologist gathered.

Specimen 1

A. aurantia, Orange-peel fungus
Color: Orange
Found near deer trail
Height of fruiting body: 12 cm

 

Specimen 2

C. argillacca, Moor-club fungus
Color: pale yellow
Height of fruiting body: 6 cm

Specimen 3

L. lubrica, jellybaby fungus
Height of fruiting body: 6 cm
Color: dark yellow

Spores present, ~ 150, each ~10 micrometres (μm)

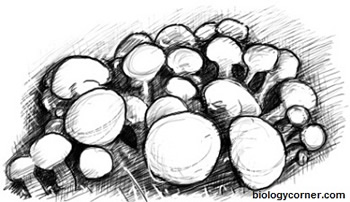
Specimen 4

P. vesiculosa, early-cup fungus
Color: white
Height of fruiting body: 7 cm

 

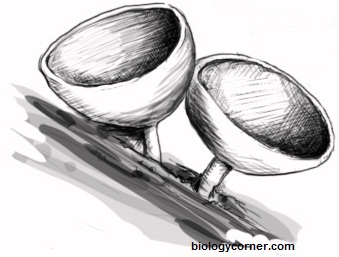
Specimen 5

X. hypoxylon,Candle-snuff fungus
Color: black and white
Found growing on a dead log
Height of fruiting body: 8 cm

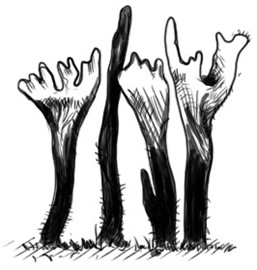
Specimen 6

M. esculenta, Morchella, true morel
Color: brown-yellow
Height of fruiting body: 14 cm

Specimen 7

R. fennica, Coral fungus
Found growing under a pine tree
Color: pink
Height of fruiting body: 5 cm